如果哪位大佬有更好的解题思路，可以互相交流一下

先看题：

看这个算式：
☆☆☆ + ☆☆☆ = ☆☆☆
如果每个五角星代表 1 ~ 9 的不同的数字。
这个算式有多少种可能的正确填写方法？
173 + 286 = 459
295 + 173 = 468
173 + 295 = 468
183 + 492 = 675
以上都是正确的填写法！
注意：
111 + 222 = 333 是错误的填写法！
因为每个数字必须是不同的！ 
也就是说：1~9中的所有数字，每个必须出现且仅出现一次！
注意：
不包括数字“0”！
注意：
满足加法交换率的式子算两种不同的答案。
所以答案肯定是个偶数！

注意：
只要求计算不同的填法的数目
不要求列出所有填写法
更不要求填写源代码！

 思路：

先用for循环循环遍历从100-999的数字，然后再把每一位数的个、十、百拿下来，利用set集合去重特性筛选1-9数字，然后输出

1.两个三位数字相加，结果还等于三位数字，所以数字范围在100 ≥ 数字 < 1000 

2.1~9数字中每个必须出现一次，第一想到的是if判断筛选，但是太复杂了需要些好多，接着又想到set集合

代码：

import java.util.HashSet;
import java.util.Set;
public class Main10 {
    public static void main(String[] args) {
        int sum = 0;
        int count = 0;
        //利用set集合去重特性筛选1~9数字
        Set<Integer> set = new HashSet<Integer>();
        //两位百位数相加的结果等于三位数  限制数字位数
        for(int i = 100; i < 1000;i++) {
            for(int j = 100; j < 1000;j++) {
                sum = i+j;
                //如果sum和不等于四位数时 跳出本次循环进入下一次
                if(sum > 1000) {
                    continue;
                }
                //将没位数的个十、百、位单独拿下来
                int a1= i /100 % 10;
                int a2= i /10 % 10;
                int a3= i % 10;

                //放进set集合中
                set.add(a1);
                set.add(a2);
                set.add(a3);

                int b1= j /100 % 10;
                int b2= j /10 % 10;
                int b3= j % 10;

                set.add(b1);
                set.add(b2);
                set.add(b3);

                int c1= sum /100 % 10;
                int c2= sum /10 % 10;
                int c3= sum % 10;

                set.add(c1);
                set.add(c2);
                set.add(c3);

                //判断长度是否等于9并且不可以包含0
                if(set.size() == 9 && !set.contains(0)) {  //contains代表可以包含  但前面有！，所以此处表示不可以包含
                    System.out.println(i+"+"+j+"="+sum);
                    //计数
                    count++;
                }
                //移除set集合中所有元素
                set.clear(); 
                /**
                 * 清空是为了 不影响 下一次的判断，如果不清空 会影响下一次的值判断
                 * 三个数字不是不能有0，但是从100开始的如果不清空下一次 循环过来set集合里面有之前的值会影响判断
                 */
            }
        }
        //计数才是答案，问题问的是有多少个而不是生成所有式子
        System.err.println(count);
    }

}

 运行结果：

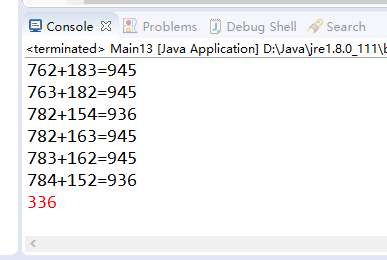
以上是《JAVA基础算法 三位五角星数相加☆☆☆ + ☆☆☆ = ☆☆☆》的全部内容，

感谢您对程序员阿鑫博客的支持！